સંપૂર્ણ સાંકળ અને સાંકળના વિભાગ માટે ઓહ્મનો કાયદો: ફોર્મ્યુલા વિકલ્પો, વર્ણન અને સમજૂતી

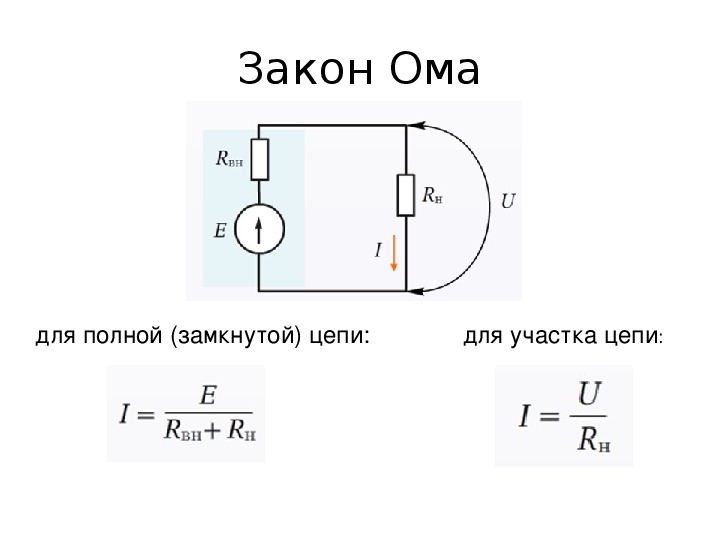
બંધ સર્કિટ માટે

ક્લોઝ્ડ સર્કિટ એટલે બંધ વિદ્યુત જોડાણ કે જેના દ્વારા કરંટ ફરે છે. જ્યારે વાયરની શ્રેણી એકબીજા સાથે જોડાય છે અને સર્કિટ પૂર્ણ કરે છે જેથી હું વર્તુળના એક છેડાથી બીજા છેડા સુધી દોડું, તે બંધ સર્કિટ હશે.

EMF (E) - વોલ્ટમાં સૂચવવામાં આવે છે અને માપવામાં આવે છે અને ફેરાડેના કાયદા અનુસાર બેટરી અથવા ચુંબકીય બળ દ્વારા ઉત્પન્ન થતા વોલ્ટેજનો સંદર્ભ આપે છે, જે જણાવે છે કે સમય-વિવિધ ચુંબકીય ક્ષેત્ર ઇલેક્ટ્રિક પ્રવાહને પ્રેરિત કરશે.

પછી: E = IR + Ir

E \u003d I (R + r)

I \u003d E / (R + r)

જ્યાં: r એ વર્તમાન સ્ત્રોતનો પ્રતિકાર છે.

આ અભિવ્યક્તિ બંધ લૂપ સર્કિટના ઓહ્મના નિયમ તરીકે ઓળખાય છે.

વિજાતીય સાંકળ

અલગ વિભાગ અને સંપૂર્ણ વિદ્યુત સર્કિટ

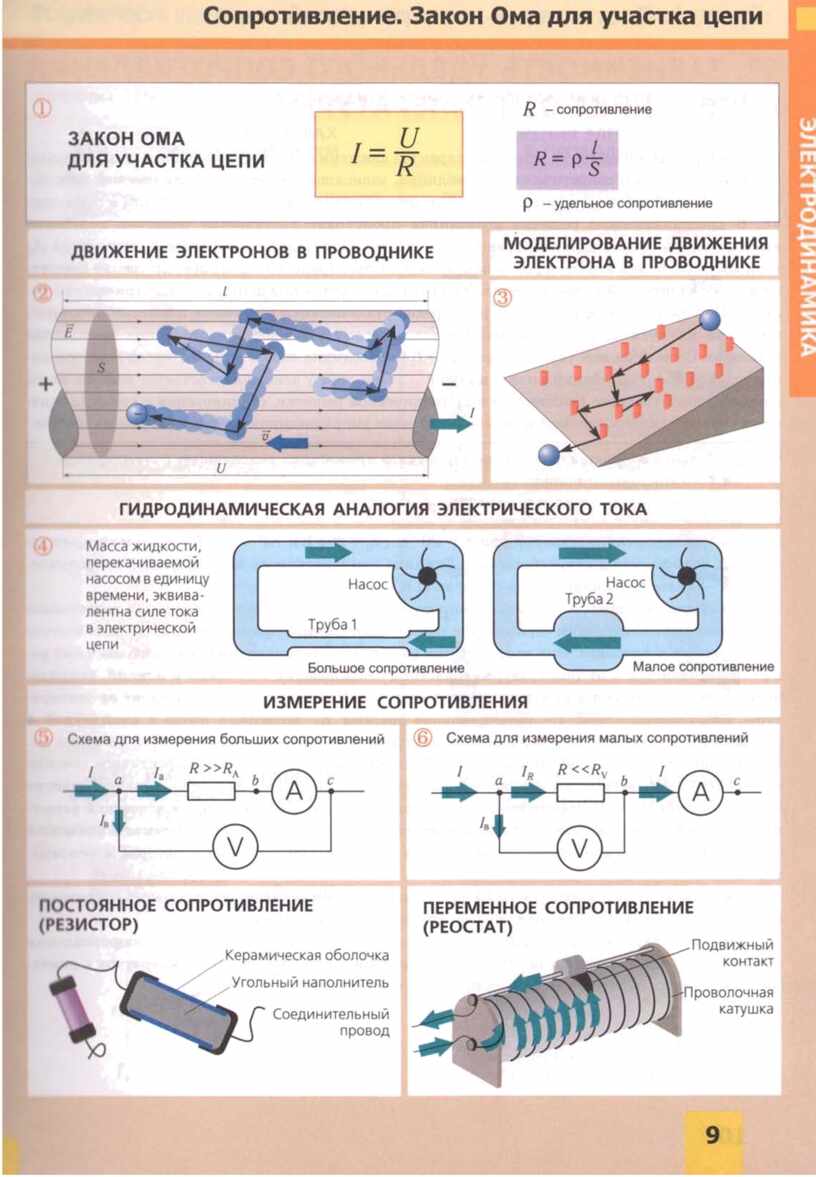
ઓહ્મનો કાયદો, જેમ કે વિભાગ અથવા સમગ્ર સર્કિટ પર લાગુ થાય છે, તેને ગણતરીના બે વિકલ્પોમાં ધ્યાનમાં લઈ શકાય છે:

• ટૂંકા વિભાગને અલગ કરો. તે EMF સ્ત્રોત વિનાના સર્કિટનો ભાગ છે.
• એક અથવા વધુ વિભાગો ધરાવતી સંપૂર્ણ સાંકળ. આમાં તેના પોતાના આંતરિક પ્રતિકાર સાથે EMF સ્ત્રોતનો પણ સમાવેશ થાય છે.

ઇલેક્ટ્રિકલ સર્કિટના વર્તમાન વિભાગની ગણતરી

આ કિસ્સામાં, મૂળભૂત સૂત્ર I \u003d U/R લાગુ કરવામાં આવે છે, જેમાં I વર્તમાન તાકાત છે, U એ વોલ્ટેજ છે, R એ પ્રતિકાર છે. તે મુજબ, કોઈ ઓહ્મના કાયદાનું સામાન્ય રીતે સ્વીકૃત અર્થઘટન ઘડી શકે છે:

આ ફોર્મ્યુલેશન ગ્રાફિક ડિઝાઇનમાં કહેવાતા "કેમોમાઇલ" પર પ્રસ્તુત અન્ય ઘણા સૂત્રો માટેનો આધાર છે. સેક્ટર P માં - પાવર નક્કી કરવામાં આવે છે, સેક્ટર I, U અને R માં - વર્તમાન તાકાત, વોલ્ટેજ અને પ્રતિકાર સંબંધિત ક્રિયાઓ હાથ ધરવામાં આવે છે.

દરેક અભિવ્યક્તિ - મૂળભૂત અને વધારાના બંને, તમને સર્કિટમાં ઉપયોગ માટે બનાવાયેલ તત્વોના ચોક્કસ પરિમાણોની ગણતરી કરવાની મંજૂરી આપે છે.

વિદ્યુત સર્કિટ સાથે કામ કરતા નિષ્ણાતો આકૃતિમાં બતાવેલ ત્રિકોણ પદ્ધતિનો ઉપયોગ કરીને કોઈપણ પરિમાણોનો ઝડપી નિર્ધારણ કરે છે.

ગણતરીઓએ વિભાગના તત્વોને જોડતા વાહકના પ્રતિકારને ધ્યાનમાં લેવું જોઈએ. તેઓ વિવિધ સામગ્રીમાંથી બનાવવામાં આવ્યા હોવાથી, આ પરિમાણ દરેક કિસ્સામાં અલગ હશે.જો સંપૂર્ણ સર્કિટ બનાવવી જરૂરી હોય, તો મુખ્ય સૂત્ર વોલ્ટેજ સ્ત્રોતના પરિમાણો સાથે પૂરક છે, ઉદાહરણ તરીકે, બેટરી.

સંપૂર્ણ સાંકળ માટે ગણતરી વિકલ્પ

સંપૂર્ણ સર્કિટમાં વ્યક્તિગત વિભાગોનો સમાવેશ થાય છે, જે વોલ્ટેજ સ્ત્રોત (EMF) સાથે એક સંપૂર્ણમાં જોડાય છે. આમ, વિભાગોનો હાલનો પ્રતિકાર કનેક્ટેડ સ્ત્રોતના આંતરિક પ્રતિકાર દ્વારા પૂરક છે. તેથી, અગાઉ ચર્ચા કરેલ મુખ્ય અર્થઘટન નીચે મુજબ વાંચશે: I = U / (R + r). અહીં, EMF સ્ત્રોતનો પ્રતિકારક સૂચક (r) પહેલેથી જ ઉમેરવામાં આવ્યો છે.

શુદ્ધ ભૌતિકશાસ્ત્રના દૃષ્ટિકોણથી, આ સૂચક ખૂબ જ નાનું મૂલ્ય માનવામાં આવે છે. જો કે, વ્યવહારમાં, જટિલ સર્કિટ અને સર્કિટની ગણતરી કરતી વખતે, નિષ્ણાતોને તેને ધ્યાનમાં લેવાની ફરજ પાડવામાં આવે છે, કારણ કે વધારાના પ્રતિકાર કાર્યની ચોકસાઈને અસર કરે છે. વધુમાં, દરેક સ્ત્રોતની રચના ખૂબ જ વિજાતીય છે, પરિણામે, કેટલાક કિસ્સાઓમાં પ્રતિકાર ખૂબ ઊંચા દરો દ્વારા વ્યક્ત કરી શકાય છે.

ઉપરોક્ત ગણતરીઓ ડીસી સર્કિટના સંબંધમાં કરવામાં આવે છે. વૈકલ્પિક પ્રવાહ સાથેની ક્રિયાઓ અને ગણતરીઓ અલગ યોજના અનુસાર કરવામાં આવે છે.

ચલ પર કાયદાની અસર

વૈકલ્પિક પ્રવાહ સાથે, સર્કિટનો પ્રતિકાર કહેવાતા અવરોધ હશે, જેમાં સક્રિય પ્રતિકાર અને પ્રતિક્રિયાશીલ પ્રતિરોધક લોડનો સમાવેશ થાય છે. આ ઇન્ડક્ટિવ પ્રોપર્ટીઝ અને સાઇનસૉઇડલ વર્તમાન મૂલ્યવાળા તત્વોની હાજરીને કારણે છે. વોલ્ટેજ પણ એક ચલ છે, જે તેના સ્વિચિંગ કાયદાઓ અનુસાર કાર્ય કરે છે.

તેથી, ઓહ્મના કાયદા અનુસાર એસી સર્કિટની ગણતરી ચોક્કસ અસરોને ધ્યાનમાં લઈને કરવામાં આવે છે: વોલ્ટેજમાંથી વર્તમાનની તીવ્રતામાં આગળ અથવા પાછળ રહે છે, તેમજ સક્રિય અને પ્રતિક્રિયાશીલ શક્તિની હાજરી.બદલામાં, પ્રતિક્રિયામાં પ્રેરક અથવા કેપેસિટીવ ઘટકોનો સમાવેશ થાય છે.

આ બધી ઘટનાઓ Z \u003d U/I અથવા Z \u003d R + J * (XL - XC) સૂત્રને અનુરૂપ હશે, જેમાં Z એ અવબાધ છે; આર - સક્રિય લોડ; XL, XC - પ્રેરક અને કેપેસિટીવ લોડ્સ; J એ કરેક્શન ફેક્ટર છે.

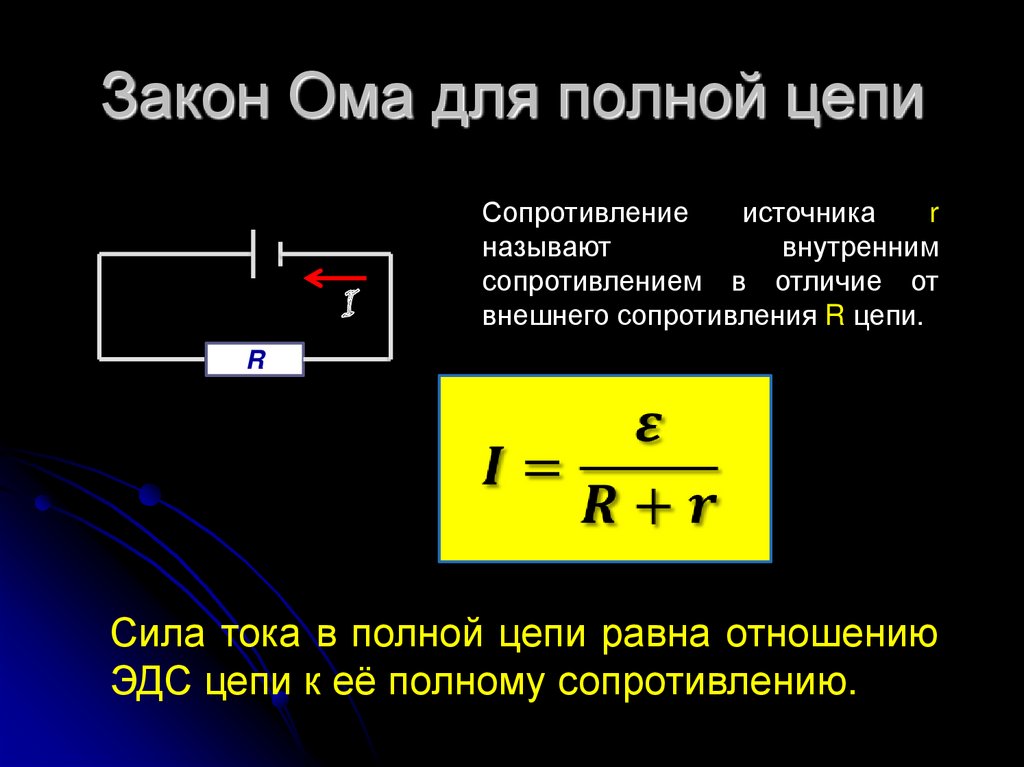
સંપૂર્ણ સર્કિટમાં EMF સ્ત્રોત

બંધ સર્કિટમાં ઇલેક્ટ્રિક પ્રવાહની ઘટના માટે, આ સર્કિટમાં ઓછામાં ઓછું એક વિશિષ્ટ તત્વ હોવું આવશ્યક છે જેમાં તેના ધ્રુવો વચ્ચે ચાર્જ ટ્રાન્સફર કરવાનું કાર્ય થશે. આ તત્વની અંદર ચાર્જ વહન કરનારા દળો ઈલેક્ટ્રિક ફિલ્ડની વિરુદ્ધ આવું કરે છે, જેનો અર્થ છે કે તેમની પ્રકૃતિ ઇલેક્ટ્રિકથી અલગ હોવી જોઈએ. તેથી, આવા દળોને તૃતીય-પક્ષ કહેવામાં આવે છે.

ચોખા. 1. ભૌતિકશાસ્ત્રમાં બાહ્ય દળો.

ઇલેક્ટ્રિકલ સર્કિટનું એક તત્વ કે જેમાં બાહ્ય દળો ઇલેક્ટ્રિક ફિલ્ડની ક્રિયા સામે ચાર્જ ટ્રાન્સફર કરવા માટે કામ કરે છે તેને વર્તમાન સ્ત્રોત કહેવામાં આવે છે. તેની મુખ્ય લાક્ષણિકતા બાહ્ય દળોની તીવ્રતા છે. તેને લાક્ષણિકતા આપવા માટે, એક વિશિષ્ટ માપ રજૂ કરવામાં આવે છે - ઇલેક્ટ્રોમોટિવ ફોર્સ (EMF), તે અક્ષર $\mathscr{E}$ દ્વારા સૂચવવામાં આવે છે.

વર્તમાન સ્ત્રોતના EMF નું મૂલ્ય આ ચાર્જના મૂલ્યમાં ચાર્જના સ્થાનાંતરણ માટે બાહ્ય દળોના ગુણોત્તર જેટલું છે:

$$\mathscr{E}={A_{st}\over q}$$

કારણ કે EMF નો અર્થ વિદ્યુત વોલ્ટેજના અર્થની ખૂબ નજીક છે (યાદ કરો, વોલ્ટેજ એ ઇલેક્ટ્રિક ક્ષેત્ર દ્વારા કરવામાં આવેલ કાર્યનો ગુણોત્તર છે જે ચાર્જને આ ચાર્જના મૂલ્ય સુધી વહન કરે છે), તો EMF, વોલ્ટેજની જેમ, માપવામાં આવે છે. વોલ્ટ:

$$1B={J\overCl}$$

વાસ્તવિક વર્તમાન સ્ત્રોતની બીજી સૌથી મહત્વપૂર્ણ વિદ્યુત લાક્ષણિકતા તેની આંતરિક પ્રતિકાર છે.જ્યારે ટર્મિનલ્સ વચ્ચે ચાર્જ ટ્રાન્સફર કરવામાં આવે છે, ત્યારે તેઓ EMF સ્ત્રોતના પદાર્થ સાથે ક્રિયાપ્રતિક્રિયા કરે છે, અને તેથી, વિદ્યુત પ્રવાહ માટેનો સ્ત્રોત થોડો પ્રતિકાર પણ રજૂ કરે છે. આંતરિક પ્રતિકાર, સામાન્ય પ્રતિકારની જેમ, ઓહ્મમાં માપવામાં આવે છે, પરંતુ નાના લેટિન અક્ષર $r$ દ્વારા સૂચવવામાં આવે છે.

ચોખા. 2. વર્તમાન સ્ત્રોતોના ઉદાહરણો.

આર - વિદ્યુત પ્રતિકાર

પ્રતિકાર એ વોલ્ટેજનો પરસ્પર છે અને તેની સરખામણી વહેતા પાણીમાં શરીરને હલનચલન સામે ખસેડવાની અસર સાથે કરી શકાય છે. R નું એકમ ઓમ છે, જે કેપિટલ ગ્રીક અક્ષર ઓમેગા દ્વારા સૂચવવામાં આવે છે.

પ્રતિકારકતા (1/R) ની પારસ્પરિકતાને વાહકતા તરીકે ઓળખવામાં આવે છે, જે સિમેન્સ એકમોમાં વ્યક્ત કરાયેલ ચાર્જ વહન કરવાની પદાર્થની ક્ષમતાને માપે છે.

વપરાયેલ ભૌમિતિક રીતે સ્વતંત્ર જથ્થાને પ્રતિકારકતા કહેવામાં આવે છે અને સામાન્ય રીતે ગ્રીક પ્રતીક r દ્વારા સૂચવવામાં આવે છે.

વધારાની માહિતી. ઓહ્મનો કાયદો વિદ્યુત નેટવર્કના સંચાલનના ત્રણ મહત્વપૂર્ણ સૂચકાંકો સ્થાપિત કરવામાં મદદ કરે છે, જે પાવરની ગણતરીને સરળ બનાવે છે. તે ડાયોડ, ટ્રાન્ઝિસ્ટર અને તેના જેવા તત્વો સાથે એકતરફી નેટવર્કને લાગુ પડતું નથી. અને તે બિન-રેખીય તત્વોને પણ લાગુ પડતું નથી, જેમાંથી thyristors ઉદાહરણો છે, કારણ કે આ તત્વોનું પ્રતિકાર મૂલ્ય અલગ અલગ આપેલ વોલ્ટેજ અને વર્તમાન સાથે બદલાય છે.

ઉચ્ચ ફ્રીક્વન્સીઝ પર, વિતરિત વર્તન પ્રબળ બને છે. આ જ વસ્તુ ખૂબ લાંબી પાવર લાઇન સાથે થાય છે. 60 હર્ટ્ઝ જેટલી ઓછી આવર્તન પર પણ, ખૂબ લાંબી ટ્રાન્સમિશન લાઇન, જેમ કે 30 કિમી, વિતરિત પ્રકૃતિ ધરાવે છે.મુખ્ય કારણ એ છે કે સર્કિટમાં પ્રસારિત થતા અસરકારક વિદ્યુત સંકેતો ઇલેક્ટ્રોમેગ્નેટિક તરંગો છે, વોલ્ટ અને એમ્પીયર નથી, જે ઇલેક્ટ્રોમેગ્નેટિક તરંગો દ્વારા ચેપગ્રસ્ત છે. વાહક ફક્ત તરંગો માટે માર્ગદર્શક તરીકે કાર્ય કરે છે. તેથી, ઉદાહરણ તરીકે, એક કોક્સિયલ કેબલ Z = 75 ઓહ્મ બતાવશે, ભલે તેનો DC પ્રતિકાર નજીવો હોય.

ઓહ્મનો કાયદો ઇલેક્ટ્રિકલ એન્જિનિયરિંગનો મૂળભૂત કાયદો છે. તે તમામ વિદ્યુત સર્કિટ અને ઇલેક્ટ્રોનિક ઘટકોમાં મોટી સંખ્યામાં પ્રાયોગિક એપ્લિકેશન ધરાવે છે.

ઓહ્મના કાયદાના ઉપયોગના સૌથી સામાન્ય ઉદાહરણો:

1. ઇલેક્ટ્રિક હીટરને આપવામાં આવતી પાવર. હીટર કોઇલના પ્રતિકાર અને લાગુ વોલ્ટેજને જોતાં, તે હીટરને આપવામાં આવતી શક્તિની ગણતરી કરી શકાય છે.
2. ફ્યુઝની પસંદગી. તે સુરક્ષા ઘટકો છે જે ઇલેક્ટ્રોનિક ઉપકરણો સાથે શ્રેણીમાં જોડાયેલા છે. ફ્યુઝ/સીબીને એમ્પ્સમાં રેટ કરવામાં આવે છે. વર્તમાન ફ્યુઝ રેટિંગ ઓહ્મના કાયદાનો ઉપયોગ કરીને ગણવામાં આવે છે.
3. ઇલેક્ટ્રોનિક ઉપકરણોની ડિઝાઇન. લેપટોપ અને મોબાઈલ ફોન જેવા ઈલેક્ટ્રોનિક ઉપકરણોને ચોક્કસ વર્તમાન રેટિંગ સાથે ડીસી પાવર સપ્લાયની જરૂર પડે છે. સામાન્ય મોબાઇલ ફોનની બેટરીઓને 0.7-1Aની જરૂર પડે છે. આ ઘટકોમાંથી વહેતા પ્રવાહના દરને નિયંત્રિત કરવા માટે રેઝિસ્ટરનો ઉપયોગ કરવામાં આવે છે. લાક્ષણિક સર્કિટમાં રેટ કરેલ પ્રવાહની ગણતરી કરવા માટે ઓહ્મનો નિયમ વપરાય છે.

એક સમયે, ઓહ્મના તારણો વીજળીના ક્ષેત્રમાં નવા સંશોધન માટે ઉત્પ્રેરક બન્યા હતા, અને આજે તેઓ તેમનું મહત્વ ગુમાવ્યા નથી, કારણ કે આધુનિક ઇલેક્ટ્રિકલ એન્જિનિયરિંગ તેમના પર આધારિત છે. 1841માં, ઓમને રોયલ સોસાયટીનું સર્વોચ્ચ સન્માન, કોપ્લી મેડલ એનાયત કરવામાં આવ્યો અને 1872ની શરૂઆતમાં "ઓમ" શબ્દને પ્રતિકારના એકમ તરીકે ઓળખવામાં આવ્યો.

ડીસી સર્કિટનો બિન-યુનિફોર્મ વિભાગ

વિજાતીય રચનામાં સર્કિટનો એવો વિભાગ હોય છે, જ્યાં વાહક અને તત્વો ઉપરાંત, વર્તમાન સ્ત્રોત હોય છે. આ વિસ્તારમાં કુલ વર્તમાન તાકાતની ગણતરી કરતી વખતે તેના EMFને ધ્યાનમાં લેવું આવશ્યક છે.

એક ફોર્મ્યુલા છે જે વિજાતીય સાઇટના મુખ્ય પરિમાણો અને પ્રક્રિયાઓને વ્યાખ્યાયિત કરે છે: q = q0 x n x V. તેના સૂચકાંકો નીચે મુજબ છે:

• ચાર્જ (q) ખસેડવાની પ્રક્રિયામાં, તેઓ ચોક્કસ ઘનતા મેળવે છે. તેનું પ્રદર્શન વર્તમાન શક્તિ અને કંડક્ટર (એસ) ના ક્રોસ-વિભાગીય ક્ષેત્ર પર આધારિત છે.
• ચોક્કસ એકાગ્રતા (n) ની શરતો હેઠળ, એક સમયગાળામાં ખસેડવામાં આવેલા એકમ શુલ્ક (q0) ની સંખ્યાને ચોક્કસ રીતે સૂચવવાનું શક્ય છે.
• ગણતરીઓ માટે, કંડક્ટરને શરતી રીતે અમુક વોલ્યુમ (V) સાથે નળાકાર વિભાગ ગણવામાં આવે છે.

કંડક્ટરને બેટરી સાથે કનેક્ટ કરતી વખતે, બાદમાં થોડા સમય પછી ડિસ્ચાર્જ કરવામાં આવશે. એટલે કે, ઇલેક્ટ્રોનની હિલચાલ ધીમે ધીમે ધીમી પડે છે અને અંતે, સંપૂર્ણપણે બંધ થઈ જાય છે. આ વાહકની પરમાણુ જાળી દ્વારા સુવિધા આપવામાં આવે છે, જે એકબીજા અને અન્ય પરિબળો સાથે ઇલેક્ટ્રોનની અથડામણનો સામનો કરે છે. આવા પ્રતિકારને દૂર કરવા માટે, અમુક તૃતીય-પક્ષ દળોને વધુમાં લાગુ કરવા જોઈએ.

ગણતરી દરમિયાન, આ દળો કુલોમ્બ રાશિઓમાં ઉમેરવામાં આવે છે. વધુમાં, એકમ ચાર્જ q ને 1લા બિંદુથી 2જીમાં સ્થાનાંતરિત કરવા માટે, કાર્ય A1-2 અથવા ફક્ત A12 કરવું જરૂરી રહેશે. આ હેતુ માટે, સંભવિત તફાવત (ϕ1 - ϕ2) બનાવવામાં આવે છે. પ્રત્યક્ષ વર્તમાન સ્ત્રોતની ક્રિયા હેઠળ, એક EMF ઉદ્ભવે છે, જે સર્કિટ સાથે ચાર્જ ખસેડે છે. કુલ તણાવની તીવ્રતામાં ઉપર નોંધેલ તમામ દળોનો સમાવેશ થશે.

ડીસી સપ્લાય સાથેના જોડાણની ધ્રુવીયતાને ગણતરીમાં ધ્યાનમાં લેવી આવશ્યક છે. જ્યારે ટર્મિનલ્સ બદલવામાં આવે છે, ત્યારે EMF પણ બદલાશે, ચાર્જની ગતિને વેગ આપશે અથવા ધીમી કરશે.

તત્વોનું સીરીયલ અને સમાંતર જોડાણ

વિદ્યુત સર્કિટ (સર્કિટનો વિભાગ) ના તત્વો માટે, લાક્ષણિકતા ક્ષણ એ શ્રેણી અથવા સમાંતર જોડાણ છે.

તદનુસાર, દરેક પ્રકારનું જોડાણ વર્તમાન પ્રવાહ અને વોલ્ટેજ પુરવઠાની અલગ પ્રકૃતિ સાથે છે. આ ખાતા પર, ઓહ્મનો કાયદો પણ અલગ અલગ રીતે લાગુ કરવામાં આવે છે, જે તત્વોને સમાવવાના વિકલ્પ પર આધાર રાખે છે.

શ્રેણી-જોડાયેલ પ્રતિકારક તત્વોની સાંકળ

શ્રેણી જોડાણ (બે ઘટકો સાથેના સર્કિટનો વિભાગ) ના સંદર્ભમાં, શબ્દોનો ઉપયોગ થાય છે:

• I = I₁ = I₂ ;
• યુ = યુ₁ + યુ₂ ;
• R=R₁ + આર₂

આ ફોર્મ્યુલેશન સ્પષ્ટપણે દર્શાવે છે કે, શ્રેણીમાં જોડાયેલા પ્રતિરોધક ઘટકોની સંખ્યાને ધ્યાનમાં લીધા વિના, સર્કિટના વિભાગમાં વહેતા પ્રવાહનું મૂલ્ય બદલાતું નથી.

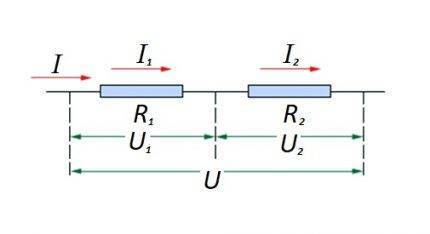સર્કિટ વિભાગમાં પ્રતિકારક તત્વોને એક બીજા સાથે શ્રેણીમાં જોડવા. આ વિકલ્પનો પોતાનો ગણતરી કાયદો છે. ડાયાગ્રામમાં: I, I1, I2 - વર્તમાન પ્રવાહ; આર 1, આર 2 - પ્રતિકારક તત્વો; U, U1, U2 - લાગુ વોલ્ટેજ

સર્કિટના સક્રિય પ્રતિકારક ઘટકો પર લાગુ વોલ્ટેજનો જથ્થો સરવાળો છે અને EMF સ્ત્રોતના મૂલ્ય સુધી ઉમેરે છે.

આ કિસ્સામાં, દરેક વ્યક્તિગત ઘટક પરનો વોલ્ટેજ છે: Ux = I * Rx.

કુલ પ્રતિકારને સર્કિટના તમામ પ્રતિકારક ઘટકોના મૂલ્યોના સરવાળા તરીકે ગણવામાં આવવો જોઈએ.

સમાંતર જોડાયેલ પ્રતિકારક તત્વોની સાંકળ

કિસ્સામાં જ્યારે પ્રતિકારક ઘટકોનું સમાંતર જોડાણ હોય, ત્યારે જર્મન ભૌતિકશાસ્ત્રી ઓહ્મના કાયદાના સંદર્ભમાં ફોર્મ્યુલેશન વાજબી માનવામાં આવે છે:

• I = I₁ + હું₂ … ;
• યુ = યુ₁ = યુ₂ … ;
• 1/R = 1/R₁ + 1 / આર₂ + …

જ્યારે સમાંતર અને સીરીયલ જોડાણોનો ઉપયોગ કરવામાં આવે ત્યારે "મિશ્રિત" પ્રકારનાં સર્કિટ વિભાગોને કમ્પાઇલ કરવાના વિકલ્પોને બાકાત રાખવામાં આવતાં નથી.

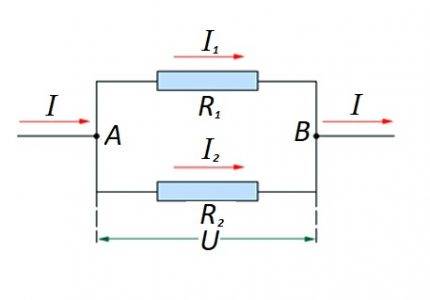એક બીજા સાથે સમાંતર સર્કિટ વિભાગમાં પ્રતિકારક તત્વોનું જોડાણ. આ વિકલ્પ માટે, તેનો પોતાનો ગણતરી કાયદો લાગુ કરવામાં આવે છે. ડાયાગ્રામમાં: I, I1, I2 - વર્તમાન પ્રવાહ; આર 1, આર 2 - પ્રતિકારક તત્વો; યુ - લાગુ વોલ્ટેજ; A, B - પ્રવેશ / બહાર નીકળવાના બિંદુઓ

આવા વિકલ્પો માટે, ગણતરી સામાન્ય રીતે સમાંતર જોડાણના પ્રતિકારક રેટિંગની પ્રારંભિક ગણતરી દ્વારા કરવામાં આવે છે. પછી શ્રેણીમાં જોડાયેલા રેઝિસ્ટરનું મૂલ્ય પરિણામમાં ઉમેરવામાં આવે છે.

કાયદાના અભિન્ન અને વિભેદક સ્વરૂપો

ગણતરીઓ સાથે ઉપરોક્ત તમામ મુદ્દાઓ એવી પરિસ્થિતિઓને લાગુ પડે છે જ્યારે "સમાન્ય" માળખાના વાહક, તેથી બોલવા માટે, ઇલેક્ટ્રિકલ સર્કિટના ભાગ રૂપે ઉપયોગમાં લેવાય છે.

દરમિયાન, વ્યવહારમાં, વ્યક્તિએ ઘણીવાર યોજનાકીય બાંધકામ સાથે વ્યવહાર કરવો પડે છે, જ્યાં કંડક્ટરની રચના વિવિધ વિસ્તારોમાં બદલાય છે. ઉદાહરણ તરીકે, મોટા ક્રોસ સેક્શનના વાયરનો ઉપયોગ કરવામાં આવે છે અથવા, તેનાથી વિપરીત, વિવિધ સામગ્રીના આધારે બનેલા નાના.

આવા તફાવતોને ધ્યાનમાં લેવા માટે, કહેવાતા "વિભેદક-અભિન્ન ઓહ્મના કાયદા" ની વિવિધતા છે. અનંત નાના વાહક માટે, વર્તમાન ઘનતા સ્તરની ગણતરી તીવ્રતા અને વાહકતા મૂલ્યના આધારે કરવામાં આવે છે.

વિભેદક ગણતરી હેઠળ, સૂત્ર લેવામાં આવે છે: J = ό * E

અવિભાજ્ય ગણતરી માટે, અનુક્રમે, ફોર્મ્યુલેશન: I * R = φ1 - φ2 + έ

જો કે, આ ઉદાહરણો ઉચ્ચ ગણિતની શાળાની વધુ નજીક છે અને વાસ્તવમાં સામાન્ય ઇલેક્ટ્રિશિયનની વાસ્તવિક પ્રેક્ટિસમાં ઉપયોગમાં લેવાતા નથી.

વર્તમાન અને પ્રતિકારને સમજવું

ચાલો વિદ્યુત પ્રવાહના ખ્યાલથી પ્રારંભ કરીએ.ટૂંકમાં, ધાતુઓના સંબંધમાં વિદ્યુત પ્રવાહ એ ઇલેક્ટ્રોનની નિર્દેશિત હિલચાલ છે - નકારાત્મક ચાર્જ કણો. તેઓ સામાન્ય રીતે નાના વર્તુળો તરીકે રજૂ થાય છે. શાંત સ્થિતિમાં, તેઓ અસ્તવ્યસ્ત રીતે આગળ વધે છે, સતત તેમની દિશા બદલતા રહે છે. ચોક્કસ પરિસ્થિતિઓમાં - સંભવિત તફાવતનો દેખાવ - આ કણો અમુક દિશામાં ચોક્કસ હિલચાલ શરૂ કરે છે. આ ચળવળ ઇલેક્ટ્રિક પ્રવાહ છે.

તેને વધુ સ્પષ્ટ કરવા માટે, અમે ઈલેક્ટ્રોનની તુલના અમુક પ્લેન પર ઢોળાતા પાણી સાથે કરી શકીએ છીએ. જ્યાં સુધી પ્લેન સ્થિર હોય ત્યાં સુધી પાણી ખસતું નથી. પરંતુ, જલદી ઢોળાવ દેખાયો (એક સંભવિત તફાવત ઊભો થયો), પાણી ખસેડવાનું શરૂ કર્યું. તે ઇલેક્ટ્રોન સાથે સમાન છે.

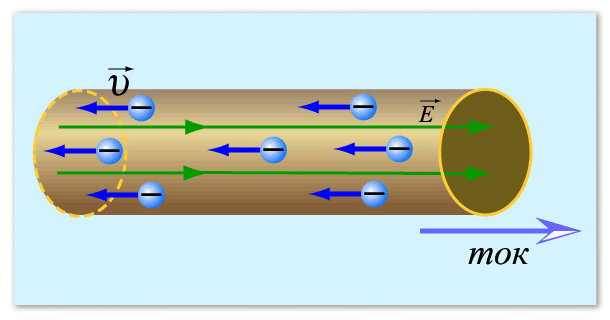
આ રીતે વિદ્યુત પ્રવાહની કલ્પના કરી શકાય છે

હવે આપણે એ સમજવાની જરૂર છે કે પ્રતિકાર શું છે અને શા માટે તેઓ વર્તમાન તાકાત સાથે પ્રતિસાદ આપે છે: પ્રતિકાર જેટલો વધારે છે, તેટલો ઓછો પ્રવાહ. જેમ તમે જાણો છો, ઇલેક્ટ્રોન વાહક દ્વારા આગળ વધે છે. સામાન્ય રીતે આ મેટલ વાયર હોય છે, કારણ કે ધાતુઓમાં વીજળીનું સંચાલન કરવાની સારી ક્ષમતા હોય છે. આપણે જાણીએ છીએ કે ધાતુમાં ગાઢ સ્ફટિક જાળી હોય છે: ઘણા કણો જે નજીકના અને એકબીજા સાથે જોડાયેલા હોય છે. ઇલેક્ટ્રોન, ધાતુના અણુઓ વચ્ચે તેમનો માર્ગ બનાવે છે, તેમની સાથે અથડાય છે, જે તેમને ખસેડવાનું મુશ્કેલ બનાવે છે. આનાથી કંડક્ટર જે પ્રતિકાર કરે છે તે દર્શાવવામાં મદદ કરે છે. હવે તે સ્પષ્ટ થઈ ગયું છે કે શા માટે પ્રતિકાર વધારે છે, વર્તમાન તાકાત ઓછી છે - વધુ કણો, ઇલેક્ટ્રોન માટે પાથ પર કાબુ મેળવવો વધુ મુશ્કેલ છે, તેઓ તે વધુ ધીમેથી કરે છે. આનો ઉકેલ આવી ગયો હોય તેમ લાગે છે.

જો તમે આ અવલંબનને પ્રયોગમૂલક રીતે ચકાસવાની ઈચ્છા ધરાવો છો, તો એક વેરિયેબલ રેઝિસ્ટર શોધો, શ્રેણીમાં રેઝિસ્ટરને કનેક્ટ કરો - એક એમીટર - વર્તમાન સ્ત્રોત (બેટરી).સર્કિટમાં સ્વીચ દાખલ કરવું પણ ઇચ્છનીય છે - એક સામાન્ય ટૉગલ સ્વીચ.

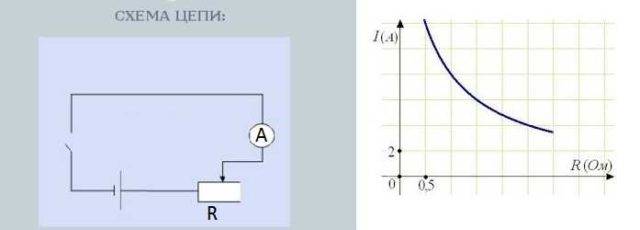
પ્રતિકાર પર વર્તમાનની અવલંબન ચકાસવા માટેનું સર્કિટ

રેઝિસ્ટર નોબ ફેરવવાથી પ્રતિકાર બદલાય છે. તે જ સમયે, એમીટર પરના રીડિંગ્સ, જે વર્તમાન તાકાતને માપે છે, તે પણ બદલાય છે. તદુપરાંત, જેટલો મોટો પ્રતિકાર, ઓછો તીર વિચલિત થાય છે - ઓછો પ્રવાહ. પ્રતિકાર ઓછો, તીર વધુ વિચલિત થાય છે - વર્તમાન વધારે છે.

પ્રતિકાર પર વર્તમાનની અવલંબન લગભગ રેખીય છે, એટલે કે, તે લગભગ સીધી રેખા તરીકે ગ્રાફ પર પ્રતિબિંબિત થાય છે. લગભગ શા માટે - આની અલગથી ચર્ચા થવી જોઈએ, પરંતુ તે બીજી વાર્તા છે.

વૈકલ્પિક પ્રવાહ માટે ઓહ્મનો કાયદો

એસી સર્કિટ્સની ગણતરી કરતી વખતે, પ્રતિકારની વિભાવનાને બદલે, "અવરોધ" ની વિભાવના રજૂ કરવામાં આવે છે. અવબાધ Z અક્ષર દ્વારા સૂચવવામાં આવે છે, તેમાં લોડ R ના સક્રિય પ્રતિકારનો સમાવેશ થાય છે_a અને પ્રતિક્રિયા X (અથવા આર_આર). આ સિનુસોઇડલ પ્રવાહના આકાર (અને અન્ય કોઈપણ સ્વરૂપોના પ્રવાહો) અને પ્રેરક તત્વોના પરિમાણો તેમજ સ્વિચિંગ કાયદાને કારણે છે:

1. ઇન્ડક્ટિવ સર્કિટમાં વર્તમાન તરત જ બદલાઈ શકતો નથી.
2. કેપેસીટન્સવાળા સર્કિટમાં વોલ્ટેજ તરત જ બદલાઈ શકતું નથી.

આમ, વર્તમાન વોલ્ટેજને લેગ અથવા લીડ કરવાનું શરૂ કરે છે, અને દેખીતી શક્તિ સક્રિય અને પ્રતિક્રિયાશીલમાં વિભાજિત થાય છે.

U=I/Z

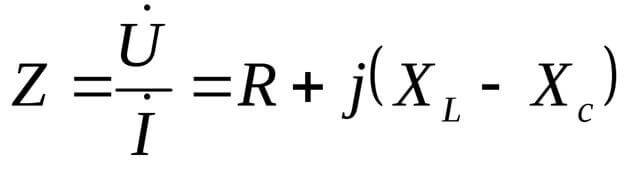
એક્સ_એલ અને એક્સ_સી લોડના પ્રતિક્રિયાશીલ ઘટકો છે.

આ સંદર્ભે, મૂલ્ય cosФ રજૂ કરવામાં આવ્યું છે:

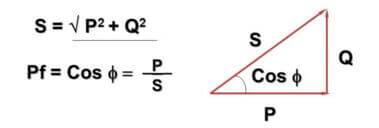
અહીં - Q - વૈકલ્પિક વર્તમાન અને ઇન્ડક્ટિવ-કેપેસિટીવ ઘટકોને કારણે પ્રતિક્રિયાશીલ શક્તિ, P - સક્રિય શક્તિ (સક્રિય ઘટકોમાં વિખરાયેલી), S - દેખીતી શક્તિ, cosФ - પાવર પરિબળ.

તમે નોંધ્યું હશે કે સૂત્ર અને તેની રજૂઆત પાયથાગોરિયન પ્રમેય સાથે છેદે છે. આ સાચું છે અને કોણ Ф લોડનો પ્રતિક્રિયાશીલ ઘટક કેટલો મોટો છે તેના પર આધાર રાખે છે - તે જેટલું મોટું છે, તેટલું મોટું છે.વ્યવહારમાં, આ એ હકીકત તરફ દોરી જાય છે કે નેટવર્કમાં વાસ્તવમાં વહેતો વર્તમાન ઘરગથ્થુ મીટર દ્વારા ધ્યાનમાં લેવામાં આવતા કરતા વધારે છે, જ્યારે સાહસો સંપૂર્ણ શક્તિ માટે ચૂકવણી કરે છે.

આ કિસ્સામાં, પ્રતિકાર જટિલ સ્વરૂપમાં રજૂ થાય છે:

અહીં j એ કાલ્પનિક એકમ છે, જે સમીકરણોના જટિલ સ્વરૂપ માટે લાક્ષણિક છે. ઓછું સામાન્ય રીતે i તરીકે ઓળખાય છે, પરંતુ વિદ્યુત ઇજનેરીમાં, વૈકલ્પિક પ્રવાહનું અસરકારક મૂલ્ય પણ સૂચવવામાં આવે છે, તેથી, મૂંઝવણમાં ન આવવા માટે, j નો ઉપયોગ કરવો વધુ સારું છે.

કાલ્પનિક એકમ √-1 છે. તે તાર્કિક છે કે વર્ગીકરણ કરતી વખતે આવી કોઈ સંખ્યા હોતી નથી, જેના પરિણામે "-1" નું નકારાત્મક પરિણામ આવી શકે.

જ્યારે ઓહ્મનો નિયમ થાય છે

આદર્શ પરિસ્થિતિઓ બનાવવી સરળ નથી. શુદ્ધ વાહકમાં પણ, વિદ્યુત પ્રતિકાર તાપમાન સાથે બદલાય છે. તેનો ઘટાડો સ્ફટિક જાળીના પરમાણુઓની પ્રવૃત્તિને ઘટાડે છે, જે મુક્ત શુલ્કની હિલચાલને સરળ બનાવે છે. "ફ્રીઝિંગ" ના ચોક્કસ સ્તરે સુપરકન્ડક્ટિવિટીની અસર થાય છે. જ્યારે ગરમ થાય છે ત્યારે વિપરીત અસર (વાહકતામાં બગાડ) જોવા મળે છે.

તે જ સમયે, ઇલેક્ટ્રોલાઇટ્સ, ધાતુઓ અને ચોક્કસ પ્રકારના સિરામિક્સ વર્તમાન ઘનતાને ધ્યાનમાં લીધા વિના વિદ્યુત પ્રતિકાર જાળવી રાખે છે. ચોક્કસ તાપમાન શાસન જાળવી રાખતી વખતે પરિમાણોની સ્થિરતા વધારાના સુધારા વિના ઓહ્મના કાયદાના સૂત્રોને લાગુ કરવાનું શક્ય બનાવે છે.

સેમિકન્ડક્ટર સામગ્રી અને વાયુઓ વિવિધ વિદ્યુત પ્રતિકાર દ્વારા વર્ગીકૃત થયેલ છે. આ પરિમાણ નિયંત્રણ વોલ્યુમમાં વર્તમાન તીવ્રતા દ્વારા નોંધપાત્ર રીતે પ્રભાવિત થાય છે. પ્રદર્શન લાક્ષણિકતાઓની ગણતરી કરવા માટે, વિશિષ્ટ ગણતરી પદ્ધતિઓ લાગુ કરવી આવશ્યક છે.

જો વૈકલ્પિક પ્રવાહ માનવામાં આવે છે, તો ગણતરી પદ્ધતિ સુધારેલ છે.આ કિસ્સામાં, પ્રતિક્રિયાશીલ ઘટકોની હાજરી ધ્યાનમાં લેવી પડશે. પ્રતિકારની પ્રતિરોધક પ્રકૃતિ સાથે, ઓહ્મના કાયદાના સૂત્રોના આધારે ગણવામાં આવતી ગણતરી તકનીકોને લાગુ કરવી શક્ય છે.

કિર્ચહોફના કાયદા.

વિતરણ
વિદ્યુત સર્કિટની શાખાઓમાં પ્રવાહો
કિર્ચહોફના પ્રથમ કાયદાનું પાલન કરે છે,
અને વિભાગો પર તણાવનું વિતરણ
સાંકળ કિર્ચહોફના બીજા કાયદાનું પાલન કરે છે.

કિર્ચહોફના કાયદા
સાથે ઓહ્મનો નિયમ મુખ્ય છે
ઇલેક્ટ્રિકલ સર્કિટના સિદ્ધાંતમાં.

પહેલું
કિર્ચહોફનો કાયદો:

બીજગણિત
નોડમાં પ્રવાહોનો સરવાળો શૂન્ય છે:

_i
= 0 (19)

જ્યાં
i
આપેલ નોડ પર એકરૂપ થતી શાખાઓની સંખ્યા છે.

એટલે કે, સમીકરણ
શાખાઓમાં પ્રવાહો સુધી વિસ્તરે છે,
જે વિચારણામાં ભેગા થાય છે
નોડ

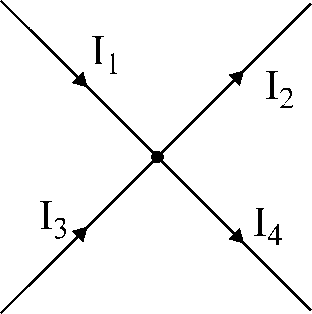
ફિગ.17. ઉદાહરણ
કિર્ચહોફના પ્રથમ કાયદાને.

નંબર
પ્રથમ અનુસાર સંકલિત સમીકરણો
કિર્ચહોફનો કાયદો સૂત્ર દ્વારા નક્કી કરવામાં આવે છે:

નૃપ
= નુ
– 1,

જ્યાં
નુ
ગણવામાં આવેલ સાંકળમાં ગાંઠોની સંખ્યા છે.

માં કરંટના ચિહ્નો
સમીકરણો પસંદ કરેલાને ધ્યાનમાં લેવામાં આવે છે
સકારાત્મક દિશા. ખાતે ચિહ્નો
જો પ્રવાહો સમાન હોય તો પ્રવાહો સમાન હોય છે
આના સંદર્ભે લક્ષી
નોડ

દાખ્લા તરીકે,
ફિગ. 17 માં બતાવેલ નોડ માટે:
અમે નોડ તરફ વહેતા પ્રવાહોને સંકેતો સોંપીએ છીએ
"+", અને નોડમાંથી વહેતા પ્રવાહો - ચિહ્નો
«-».

પછી સમીકરણ
કિર્ચહોફના પ્રથમ કાયદા અનુસાર, તે લખવામાં આવશે
તેથી:

આઈ₁
- આઇ₂
+ હું₃
- આઇ₄
= 0.

સમીકરણો
કિર્ચહોફના પ્રથમ કાયદા અનુસાર સંકલિત,
નોડ કહેવાય છે.

આ
કાયદો એ હકીકતને વ્યક્ત કરે છે કે નોડમાં
ઇલેક્ટ્રિક ચાર્જ એકઠું થતું નથી
અને વપરાશ થતો નથી. વિદ્યુત જથ્થો
સાઈટ પર આવતા શુલ્ક સરવાળે છે
નોડને એકમાં છોડીને ચાર્જ કરે છે
સમાન સમયગાળો.

બીજું
કિર્ચહોફનો કાયદો:

બીજગણિત
emf નો સરવાળો કોઈપણ બંધ સર્કિટમાં
સાંકળ ધોધના બીજગણિત સરવાળા જેટલી છે
આ સર્કિટના તત્વો પર વોલ્ટેજ:

Ui
= 
ઇઇ

IiRi=Ei(20)

જ્યાં
i
- તત્વ નંબર (પ્રતિકાર અથવા
વોલ્ટેજ સ્ત્રોત) ધ્યાનમાં લેવામાં આવે છે
સમોચ્ચ

**નંબર
બીજા અનુસાર સંકલિત સમીકરણો
કિર્ચહોફનો કાયદો સૂત્ર દ્વારા નક્કી કરવામાં આવે છે:

નૃપ
= Nb
- નુ
+ 1 – Ned.s.

જ્યાં
Nb
- ઇલેક્ટ્રિકલ સર્કિટની શાખાઓની સંખ્યા;

નુ
- ગાંઠોની સંખ્યા;

Ned.s.
આદર્શ emf સ્ત્રોતોની સંખ્યા છે.

ફિગ.18. ઉદાહરણ
કિર્ચહોફના બીજા કાયદા માટે.

માટે,
બીજો કાયદો યોગ્ય રીતે લખવા માટે
આપેલ સમોચ્ચ માટે કિર્ચહોફ, નીચે મુજબ છે
નીચેના નિયમોનું પાલન કરો:

1. મનસ્વી રીતે
   સમોચ્ચ બાયપાસની દિશા પસંદ કરો,
   ઉદાહરણ તરીકે, ઘડિયાળની દિશામાં (ફિગ. 18).

2. emf
   અને વોલ્ટેજ ડ્રોપ્સ જે મેચ થાય છે
   પસંદ કરેલ દિશા સાથે દિશામાં
   બાયપાસ સાથે અભિવ્યક્તિમાં લખાયેલ છે
   ચિહ્ન "+"; જો ઇ.એફ.એસ. અને વોલ્ટેજ ડ્રોપ
   દિશા મેળ ખાતી નથી
   સમોચ્ચ, પછી તેઓ એક ચિહ્ન દ્વારા આગળ આવે છે
   «-».

દાખ્લા તરીકે,
ફિગ. 18 ના સમોચ્ચ માટે, કિર્ચહોફનો બીજો કાયદો
નીચે પ્રમાણે લખવામાં આવશે:

યુ₁
- યુ₂
+ યુ₃
= ઇ₁
- ઇ₃
- ઇ₄
(21)

સમીકરણ (20) હોઈ શકે છે
આ રીતે ફરીથી લખો:

 (Ui
- Ei)
= 0 (22)

જ્યાં
(યુ
– ઇ)
- શાખા પર તણાવ.

પરિણામે,
કિર્ચહોફનો બીજો કાયદો ઘડી શકાય છે
નીચેની રીતે:

બીજગણિત
કોઈપણ શાખાઓ પરના વોલ્ટેજનો સરવાળો
બંધ લૂપ શૂન્ય છે.

સંભવિત
અગાઉ ચર્ચા કરેલ રેખાકૃતિ સેવા આપે છે
બીજાનું ગ્રાફિકલ અર્થઘટન
કિર્ચહોફનો કાયદો.

કાર્ય નંબર 1.

એટી
ફિગ. 1 માં સર્કિટ I કરંટ આપેલ છે₁
અને હું₃,
પ્રતિકાર અને ઇએમએફ પ્રવાહો નક્કી કરો
આઈ₄,
આઈ₅,
આઈ₆
; પોઈન્ટ વચ્ચે વોલ્ટેજ a
અને બી
જો હું₁
= 10mA,
આઈ₃
= -20 એમએ,
આર₄
= 5kOhm,
ઇ₅
= 20B,
આર₅
= 3kOhm,
ઇ₆
= 40B,
આર₆
= 2kOhm.

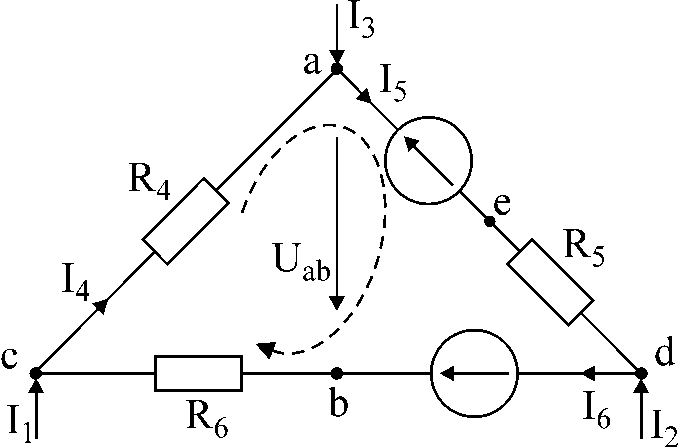
ફિગ.1

ઉકેલ:

1. આપેલ માટે
   સમોચ્ચ, અમે બે સમીકરણો અનુસાર કંપોઝ કરીએ છીએ
   Kirchhoff પ્રથમ કાયદો અને એક - અનુસાર
   બીજું સમોચ્ચ દિશા
   તીર દ્વારા દર્શાવેલ.

એટી
ઉકેલના પરિણામે આપણને મળે છે: I₆
= 0; આઈ₄
= 10mA;
આઈ₅
= -10mA

1. પુછવું
   પોઈન્ટ વચ્ચે વોલ્ટેજ દિશા
   a
   અને બી
   બિંદુ "a" થી
   નિર્દેશ કરવા માટે "b"
   - યુ_ab.
   આ વોલ્ટેજ સમીકરણમાંથી શોધી શકાય છે
   કિર્ચહોફનો બીજો કાયદો:

આઈ₄આર₄
+ યુ_ab
+ હું₆આર₆
= 0

યુ_ab
= - 50V.

કાર્ય નંબર 2.

માટે
ફિગ. 2 માં આકૃતિઓ અનુસાર સમીકરણો દોરે છે
કિર્ચહોફના કાયદા અને અજાણ્યાઓ નક્કી કરે છે
પોઈન્ટ

આપેલ:
આઈ₁
= 20mA;
આઈ₂
= 10mA

આર₁
= 5kOhm,
આર₃
= 4kOhm,
આર₄
= 6kOhm,
આર₅
= 2kOhm,
આર₆
= 4kΩ.

ફિગ.2

ઉકેલ:

નોડ્સની સંખ્યા
સમીકરણો - 3, સમોચ્ચ સમીકરણોની સંખ્યા
– 1.

યાદ રાખો!
જ્યારે બીજા મુજબ સમીકરણનું સંકલન કરો
કિર્ચહોફનો કાયદો, અમે સમોચ્ચ પસંદ કરીએ છીએ, માં
જેમાં વર્તમાન સ્ત્રોતોનો સમાવેશ થતો નથી.
સમોચ્ચની દિશા આકૃતિમાં દર્શાવેલ છે.

એટી
આ સર્કિટના, શાખાઓના પ્રવાહો I₁
અને હું₂.
અજ્ઞાત
પ્રવાહો
આઈ₃,
આઈ₄,
આઈ₅,
આઈ₆.

નક્કી કરે છે
સિસ્ટમ, અમને મળે છે: I₃
= 13.75 એમએ;
આઈ₄
= -3.75mA;
આઈ₅
= 6.25mA;
આઈ₆
= 16.25mA.

મૂળભૂત ખ્યાલો

જ્યારે ક્લોઝ્ડ સર્કિટ ઈલેક્ટ્રોનને સર્કિટમાં ઉચ્ચ સંભવિતમાંથી નીચલા એક તરફ જવા દે છે ત્યારે ઇલેક્ટ્રિક પ્રવાહ વહે છે. બીજા શબ્દોમાં કહીએ તો, વિદ્યુતપ્રવાહને ઈલેક્ટ્રોનના સ્ત્રોતની જરૂર હોય છે જે તેમને ગતિમાં ગોઠવવા માટે ઊર્જા ધરાવે છે, તેમજ તેમના નકારાત્મક ચાર્જના વળતરનો એક બિંદુ, જે તેમની ઉણપ દ્વારા વર્ગીકૃત થયેલ છે. ભૌતિક ઘટના તરીકે, સર્કિટમાં વર્તમાન ત્રણ મૂળભૂત જથ્થાઓ દ્વારા વર્ગીકૃત થયેલ છે:

• વિદ્યુત્સ્થીતિમાન;
• વર્તમાન તાકાત;
• વાહકનો પ્રતિકાર કે જેના દ્વારા ઇલેક્ટ્રોન ખસેડે છે.

તાકાત અને તાણ

વર્તમાન તાકાત (I, એમ્પીયરમાં માપવામાં આવે છે) એ સમયના એકમ દીઠ સર્કિટમાં એક જગ્યાએથી ફરતા ઇલેક્ટ્રોન (ચાર્જ) નું પ્રમાણ છે.બીજા શબ્દોમાં કહીએ તો, માપ I એ ગતિમાં રહેલા ઇલેક્ટ્રોનની સંખ્યાનું નિર્ધારણ છે

તે સમજવું અગત્યનું છે કે આ શબ્દ માત્ર ચળવળનો સંદર્ભ આપે છે: સ્થિર ચાર્જ, ઉદાહરણ તરીકે, બિનજોડાણ વગરની બેટરીના ટર્મિનલ્સ પર, I નું માપી શકાય તેવું મૂલ્ય હોતું નથી. વર્તમાન જે એક દિશામાં વહે છે તેને ડાયરેક્ટ (DC) કહેવાય છે, અને સમયાંતરે દિશા બદલવાને વૈકલ્પિક (AC) કહેવાય છે. વોલ્ટેજને દબાણ જેવી ઘટના દ્વારા અથવા ગુરુત્વાકર્ષણના પ્રભાવ હેઠળના પદાર્થોની સંભવિત ઊર્જામાં તફાવત તરીકે દર્શાવી શકાય છે.

આ અસંતુલન બનાવવા માટે, તમારે સૌપ્રથમ ઉર્જાનો ખર્ચ કરવો પડશે, જે યોગ્ય સંજોગોમાં ગતિમાં સાકાર થશે. ઉદાહરણ તરીકે, ઊંચાઈ પરથી લોડ પડતાં, તેને ઉપાડવાનું કામ હાથ ધરવામાં આવે છે, ગેલ્વેનિક બેટરીમાં, ટર્મિનલ્સ પર સંભવિત તફાવત રાસાયણિક ઊર્જાના રૂપાંતરણને કારણે રચાય છે, જનરેટરમાં - એક્સપોઝરના પરિણામે. ઇલેક્ટ્રોમેગ્નેટિક ક્ષેત્ર

તણાવને દબાણ જેવી ઘટના દ્વારા અથવા ગુરુત્વાકર્ષણના પ્રભાવ હેઠળના પદાર્થોની સંભવિત ઊર્જામાં તફાવત તરીકે દર્શાવી શકાય છે. આ અસંતુલન બનાવવા માટે, તમારે સૌપ્રથમ ઉર્જાનો ખર્ચ કરવો પડશે, જે યોગ્ય સંજોગોમાં ગતિમાં સાકાર થશે. ઉદાહરણ તરીકે, ઊંચાઈ પરથી લોડ પડતાં, તેને ઉપાડવાનું કામ સાકાર થાય છે, ગેલ્વેનિક બેટરીમાં ટર્મિનલ્સમાં સંભવિત તફાવત રાસાયણિક ઉર્જાના રૂપાંતરણને કારણે રચાય છે, જનરેટરમાં - એક્સપોઝરના પરિણામે. ઇલેક્ટ્રોમેગ્નેટિક ક્ષેત્ર.

વાહક પ્રતિકાર

સામાન્ય વાહક ગમે તેટલો સારો હોય, તે ઇલેક્ટ્રોનને તેમની હિલચાલના કેટલાક પ્રતિકાર વિના ક્યારેય પસાર થવા દેશે નહીં.યાંત્રિક ઘર્ષણના એનાલોગ તરીકે પ્રતિકારને ધ્યાનમાં લેવું શક્ય છે, જો કે આ સરખામણી સંપૂર્ણ રહેશે નહીં. જ્યારે વાહકમાંથી પ્રવાહ વહે છે, ત્યારે કેટલાક સંભવિત તફાવતને ગરમીમાં રૂપાંતરિત કરવામાં આવે છે, તેથી રેઝિસ્ટરમાં હંમેશા વોલ્ટેજ ડ્રોપ રહેશે. ઇલેક્ટ્રિક હીટર, હેર ડ્રાયર્સ અને અન્ય સમાન ઉપકરણો માત્ર ગરમીના સ્વરૂપમાં વિદ્યુત ઉર્જાને દૂર કરવા માટે ડિઝાઇન કરવામાં આવ્યા છે.

સરળ પ્રતિકાર (R તરીકે સૂચવવામાં આવે છે) એ એક માપ છે કે સર્કિટમાં ઇલેક્ટ્રોનનો પ્રવાહ કેટલો મંદ છે. તે ઓહ્મમાં માપવામાં આવે છે. રેઝિસ્ટર અથવા અન્ય તત્વની વાહકતા બે ગુણધર્મો દ્વારા નક્કી કરવામાં આવે છે:

• ભૂમિતિ;
• સામગ્રી

હાઇડ્રોલિક સામ્યતા પરથી સ્પષ્ટ થાય છે કે આકાર અત્યંત મહત્વનો છે: ટૂંકા અને પહોળા પાઇપમાંથી પાણીને આગળ ધકેલવા કરતાં લાંબા અને સાંકડા પાઇપમાંથી પાણીને ધકેલવું ઘણું અઘરું છે. સામગ્રી નિર્ણાયક ભૂમિકા ભજવે છે. ઉદાહરણ તરીકે, ઇલેક્ટ્રોન તાંબાના વાયરમાં મુક્તપણે ખસેડી શકે છે, પરંતુ તેમના આકારને ધ્યાનમાં લીધા વિના, રબર જેવા ઇન્સ્યુલેટર દ્વારા બિલકુલ વહેતા નથી. ભૂમિતિ અને સામગ્રી ઉપરાંત, અન્ય પરિબળો છે જે વાહકતાને અસર કરે છે.

ઓહ્મના કાયદાનું અર્થઘટન

શુલ્કની હિલચાલની ખાતરી કરવા માટે, તમારે સર્કિટ બંધ કરવાની જરૂર છે. વધારાની શક્તિની ગેરહાજરીમાં, વર્તમાન લાંબા સમય સુધી અસ્તિત્વમાં નથી. સંભાવનાઓ ઝડપથી સમાન બની જશે. સર્કિટના ઓપરેટિંગ મોડને જાળવવા માટે, વધારાના સ્ત્રોત (જનરેટર, બેટરી) ની જરૂર છે.

સંપૂર્ણ સર્કિટમાં તમામ ઘટકોનો કુલ વિદ્યુત પ્રતિકાર હશે. સચોટ ગણતરીઓ માટે, કંડક્ટર, પ્રતિરોધક તત્વો અને પાવર સ્ત્રોતમાં થયેલા નુકસાનને ધ્યાનમાં લેવામાં આવે છે.

ચોક્કસ વર્તમાન તાકાત માટે કેટલો વોલ્ટેજ લાગુ કરવાની જરૂર છે તેની ગણતરી સૂત્ર દ્વારા કરવામાં આવે છે:

U=I*R.

એ જ રીતે, માનવામાં આવતા સંબંધોની મદદથી, સર્કિટના અન્ય પરિમાણો નક્કી કરવામાં આવે છે.

સમાંતર અને સીરીયલ જોડાણ

ઇલેક્ટ્રીક્સમાં, તત્વો કાં તો શ્રેણીમાં જોડાયેલા હોય છે - એક પછી એક, અથવા સમાંતર - આ ત્યારે થાય છે જ્યારે ઘણા ઇનપુટ એક બિંદુ સાથે જોડાયેલા હોય છે, અને સમાન તત્વોમાંથી આઉટપુટ બીજા સાથે જોડાયેલા હોય છે.

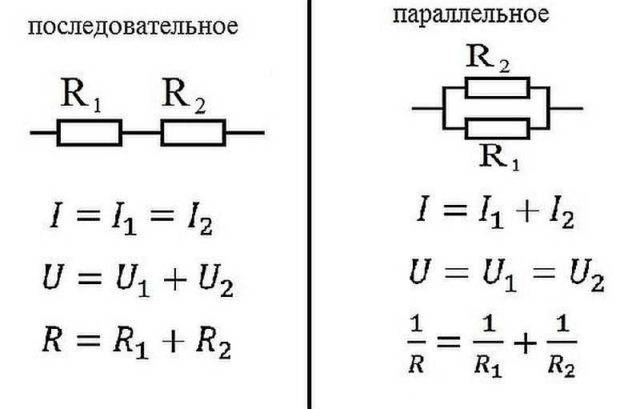
સમાંતર અને શ્રેણી જોડાણ માટે ઓહ્મનો કાયદો

સીરીયલ કનેક્શન

આ કેસ માટે ઓહ્મનો કાયદો કેવી રીતે કામ કરે છે? જ્યારે શ્રેણીમાં જોડાયેલ હોય, ત્યારે તત્વોની સાંકળમાંથી વહેતો પ્રવાહ સમાન હશે. શ્રેણીમાં જોડાયેલા તત્વો સાથે સર્કિટના વિભાગના વોલ્ટેજની ગણતરી દરેક વિભાગમાં વોલ્ટેજના સરવાળા તરીકે કરવામાં આવે છે. આ કેવી રીતે સમજાવી શકાય? તત્વ દ્વારા પ્રવાહનો પ્રવાહ એ તેના એક ભાગમાંથી બીજા ભાગમાં ચાર્જના ભાગનું ટ્રાન્સફર છે. મારો મતલબ, તે થોડું કામ છે. આ કાર્યની તીવ્રતા તણાવ છે. આ તણાવનો ભૌતિક અર્થ છે. જો આ સ્પષ્ટ છે, તો અમે આગળ વધીએ છીએ.

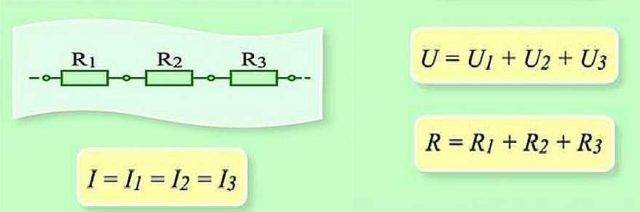
સર્કિટના આ વિભાગના સીરીયલ કનેક્શન અને પરિમાણો

જ્યારે શ્રેણીમાં જોડાયેલ હોય, ત્યારે દરેક તત્વ દ્વારા બદલામાં ચાર્જ સ્થાનાંતરિત કરવું જરૂરી છે. અને દરેક તત્વ પર, આ કાર્યનું ચોક્કસ "વોલ્યુમ" છે. અને સાંકળના સમગ્ર વિભાગ પર કાર્યની માત્રા શોધવા માટે, તમારે દરેક ઘટક પર કાર્ય ઉમેરવાની જરૂર છે. તેથી તે તારણ આપે છે કે કુલ વોલ્ટેજ એ દરેક તત્વો પરના વોલ્ટેજનો સરવાળો છે.

એ જ રીતે - ઉમેરાની મદદથી - સર્કિટ વિભાગનો કુલ પ્રતિકાર પણ જોવા મળે છે. તમે તેની કલ્પના કેવી રીતે કરી શકો? તત્વોની સાંકળમાંથી વહેતો પ્રવાહ ક્રમિક રીતે તમામ પ્રતિકારને દૂર કરે છે. એક પછી એક. એટલે કે, તેણે જે પ્રતિકાર મેળવ્યો તે શોધવા માટે, પ્રતિકાર ઉમેરવા જરૂરી છે. આના જેવા વધુ કે ઓછા.ગાણિતિક વ્યુત્પત્તિ વધુ જટિલ છે, અને આ કાયદાની પદ્ધતિને સમજવી સરળ છે.

સમાંતર જોડાણ

સમાંતર જોડાણ એ છે જ્યારે વાહક/તત્વોની શરૂઆત એક બિંદુએ એકત્ર થાય છે, અને બીજા સ્થાને તેમના છેડા જોડાયેલા હોય છે. અમે આ પ્રકારના સંયોજનો માટે માન્ય કાયદાઓ સમજાવવાનો પ્રયત્ન કરીશું. ચાલો વર્તમાન સાથે પ્રારંભ કરીએ. તત્વોના જોડાણ બિંદુને અમુક તીવ્રતાનો પ્રવાહ પૂરો પાડવામાં આવે છે. તે અલગ પડે છે, બધા વાહક દ્વારા વહે છે. આમાંથી આપણે નિષ્કર્ષ પર આવીએ છીએ કે વિભાગમાં કુલ વર્તમાન દરેક ઘટકોમાં વર્તમાનના સરવાળા સમાન છે: I = I1 + I2 + I3.

હવે વોલ્ટેજ માટે. જો વોલ્ટેજ એ ચાર્જને ખસેડવા માટેનું કાર્ય છે, તો પછી એક ચાર્જને ખસેડવા માટે જે કાર્ય જરૂરી છે તે કોઈપણ તત્વ પર સમાન હશે. એટલે કે, દરેક સમાંતર જોડાયેલ તત્વ પરનો વોલ્ટેજ સમાન હશે. U=U1=U2=U3. સાંકળ વિભાગ માટે ઓહ્મના કાયદાની સમજૂતીના કિસ્સામાં જેટલું મનોરંજક અને દ્રશ્ય નથી, પરંતુ તમે સમજી શકો છો.

સમાંતર જોડાણ માટેના કાયદા

પ્રતિકાર માટે, વસ્તુઓ થોડી વધુ જટિલ છે. ચાલો વાહકતાનો ખ્યાલ રજૂ કરીએ. આ એક લાક્ષણિકતા છે જે દર્શાવે છે કે આ વાહકમાંથી ચાર્જ પસાર કરવું કેટલું સરળ અથવા મુશ્કેલ છે. તે સ્પષ્ટ છે કે પ્રતિકાર જેટલો ઓછો હશે, તે વર્તમાન પસાર કરવા માટે સરળ હશે. તેથી, વાહકતા - જી - પ્રતિકારના પારસ્પરિક તરીકે ગણવામાં આવે છે. સૂત્રમાં, તે આના જેવું દેખાય છે: G = 1/R.

શા માટે આપણે વાહકતા વિશે વાત કરી રહ્યા છીએ? કારણ કે તત્વોના સમાંતર જોડાણવાળા વિભાગની કુલ વાહકતા દરેક વિભાગ માટે વાહકતાના સરવાળા જેટલી હોય છે. G = G1 + G2 + G3 - સમજવામાં સરળ. વર્તમાન સમાંતર તત્વોના આ માળખાને કેટલી સરળતાથી દૂર કરશે તે દરેક તત્વોની વાહકતા પર આધાર રાખે છે. તેથી તે તારણ આપે છે કે તેમને ફોલ્ડ કરવાની જરૂર છે.

હવે આપણે પ્રતિકાર તરફ આગળ વધી શકીએ છીએ.કારણ કે વાહકતા એ પ્રતિકારનો પરસ્પર છે, આપણે નીચેનું સૂત્ર મેળવી શકીએ છીએ: 1/R = 1/R1 + 1/R2 + 1/R3.

શું આપણને સમાંતર અને સીરીયલ જોડાણ આપે છે?

સૈદ્ધાંતિક જ્ઞાન સારું છે, પરંતુ વ્યવહારમાં કેવી રીતે લાગુ કરવું? કોઈપણ પ્રકારના તત્વોને સમાંતર અને શ્રેણીમાં જોડી શકાય છે. પરંતુ અમે રેખીય તત્વોનું વર્ણન કરતા માત્ર સરળ સૂત્રોને જ ગણ્યા. રેખીય તત્વો પ્રતિકાર છે, જેને "રેઝિસ્ટર" પણ કહેવામાં આવે છે. તો તમે જે શીખ્યા તેનો ઉપયોગ તમે કેવી રીતે કરી શકો તે અહીં છે:

જો ત્યાં કોઈ મોટા-મૂલ્યવાળા રેઝિસ્ટર ઉપલબ્ધ ન હોય, પરંતુ ત્યાં ઘણા નાના હોય, તો શ્રેણીમાં કેટલાક રેઝિસ્ટરને જોડીને ઇચ્છિત પ્રતિકાર મેળવી શકાય છે. જેમ તમે જોઈ શકો છો, આ એક ઉપયોગી યુક્તિ છે.
બેટરીના જીવનને વધારવા માટે, તેઓ સમાંતર રીતે કનેક્ટ થઈ શકે છે. આ કિસ્સામાં, વોલ્ટેજ, ઓહ્મના કાયદા અનુસાર, સમાન રહેશે (તમે મલ્ટિમીટર સાથે વોલ્ટેજને માપીને ખાતરી કરી શકો છો). અને દ્વિ બેટરીનું "જીવનકાળ" બે ઘટકો કરતાં ઘણું લાંબુ હશે જે એકબીજાને બદલશે

ફક્ત નોંધ કરો: સમાન સંભવિત સાથે માત્ર પાવર સપ્લાય સમાંતર રીતે કનેક્ટ કરી શકાય છે. એટલે કે, ડેડ અને નવી બેટરી કનેક્ટ કરી શકાતી નથી.

જો તમે હજી પણ કનેક્ટ કરો છો, તો જે બેટરી વધુ ચાર્જ કરે છે તે ઓછી ચાર્જ કરેલી બેટરી ચાર્જ કરશે. પરિણામે, તેમનો કુલ ચાર્જ નીચા મૂલ્ય પર આવી જશે.

સામાન્ય રીતે, આ સંયોજનો માટે આ સૌથી સામાન્ય ઉપયોગો છે.

આદર્શ EMF સ્ત્રોત

ઇલેક્ટ્રોમોટિવ ફોર્સ (ઇ) એ ભૌતિક જથ્થો છે જે ચાર્જ કેરિયર્સના બંધ સર્કિટમાં ચળવળ પર બાહ્ય દળોના પ્રભાવની ડિગ્રી નક્કી કરે છે. બીજા શબ્દોમાં કહીએ તો, વાહકમાંથી વર્તમાન કેટલી મજબૂત રીતે વહે છે તે EMF પર નિર્ભર રહેશે.

આવી અગમ્ય ઘટના સમજાવતી વખતે, ઘરેલું શાળાના શિક્ષકો હાઇડ્રોલિક સામ્યતાની પદ્ધતિ તરફ વળવાનું પસંદ કરે છે. જો વાહક એક પાઇપ છે, અને ઇલેક્ટ્રિક પ્રવાહ તેમાંથી વહેતા પાણીનું પ્રમાણ છે, તો EMF એ દબાણ છે જે પંપ પ્રવાહીને પંપ કરવા માટે વિકસાવે છે.

ઇલેક્ટ્રોમોટિવ ફોર્સ શબ્દ વોલ્ટેજ જેવા ખ્યાલ સાથે સંબંધિત છે. તેણી, ઇએમએફ, વોલ્ટમાં પણ માપવામાં આવે છે (એકમ - "વી"). દરેક પાવર સ્ત્રોત, પછી તે બેટરી હોય, જનરેટર હોય કે સૌર પેનલ હોય, તેનું પોતાનું ઇલેક્ટ્રોમોટિવ બળ હોય છે. ઘણીવાર આ EMF આઉટપુટ વોલ્ટેજ (U) ની નજીક હોય છે, પરંતુ હંમેશા તેનાથી થોડું ઓછું હોય છે. આ સ્ત્રોતના આંતરિક પ્રતિકારને કારણે થાય છે, જેના પર વોલ્ટેજનો ભાગ અનિવાર્યપણે ડ્રોપ થાય છે.

આ કારણોસર, ઇએમએફનો આદર્શ સ્ત્રોત એ તેના બદલે એક અમૂર્ત ખ્યાલ અથવા ભૌતિક મોડેલ છે જેનું વાસ્તવિક વિશ્વમાં કોઈ સ્થાન નથી, કારણ કે બેટરી રિનનો આંતરિક પ્રતિકાર, ખૂબ ઓછો હોવા છતાં, સંપૂર્ણ શૂન્યથી અલગ છે.

ઇએમએફનો આદર્શ અને વાસ્તવિક સ્ત્રોત

વિભેદક સ્વરૂપમાં

સૂત્ર ઘણીવાર વિભેદક સ્વરૂપમાં રજૂ કરવામાં આવે છે, કારણ કે વાહક સામાન્ય રીતે અસંગત હોય છે અને તેને શક્ય તેટલા નાના ભાગોમાં તોડવું જરૂરી રહેશે. તેમાંથી પસાર થતો વિદ્યુતપ્રવાહ તીવ્રતા અને દિશા સાથે સંકળાયેલો છે, તેથી તેને સ્કેલર જથ્થા તરીકે ગણવામાં આવે છે. જ્યારે પણ વાયર દ્વારા પરિણામી પ્રવાહ શોધવામાં આવે છે, ત્યારે તમામ વ્યક્તિગત પ્રવાહોનો બીજગણિત સરવાળો લેવામાં આવે છે. આ નિયમ માત્ર સ્કેલર જથ્થાને લાગુ પડતો હોવાથી, વર્તમાનને પણ સ્કેલર જથ્થા તરીકે લેવામાં આવે છે. તે જાણીતું છે કે વર્તમાન dI = jdS વિભાગમાંથી પસાર થાય છે. તેના પરનું વોલ્ટેજ એડીએલ જેટલું છે, પછી સતત ક્રોસ સેક્શન અને સમાન લંબાઈવાળા વાયર માટે, ગુણોત્તર સાચું હશે:

વિભેદક સ્વરૂપ

તેથી, વેક્ટર સ્વરૂપમાં વર્તમાનની અભિવ્યક્તિ હશે: j = E.

મહત્વપૂર્ણ! મેટાલિક કંડક્ટરના કિસ્સામાં, વધતા તાપમાન સાથે વાહકતા ઘટે છે, જ્યારે સેમિકન્ડક્ટર માટે તે વધે છે. ઓમોવનો કાયદો કડક પ્રમાણસરતા દર્શાવતો નથી

ધાતુઓ અને એલોયના મોટા જૂથનો પ્રતિકાર સંપૂર્ણ શૂન્યની નજીકના તાપમાને અદૃશ્ય થઈ જાય છે, અને પ્રક્રિયાને સુપરકન્ડક્ટિવિટી કહેવામાં આવે છે.